5.21. Treatment of physical units¶
Within equations for calculating the value of an output quantity, the input quantities are fully described by a value and by a unit. Sometimes, it is not fully considered that instead of basic units (such as kg, m, s) derived units (such as g, cm, min) are used. For calculating the output quantity value correctly, with a combination of basic units as its unit, scale factors for derived units have to be inserted in the equations. There are two concepts supporting this within UncertRadio:
Application of Trigger variables used to explicitly introduce unit scaling factors in equations; the reader is referred to section 7.21.5. The scope of application of such triggers normally is wider than its use for scale factors.
One can try to derive the unit of a dependent quantity from the units of its input quantities by computations. This method can be used within UncertRadio, at present mainly designed as a testing option for a project. The more detailed description of such a method is the main purpose of this section.
Therefore, the aim is to correctly define for a project the number values and units of its input quantities. This also includes the use of derived units. It should then be possible for the program, to derive the unit of the output quantity, with including the conversion to basic units of the output quantity.
For successfully going this way, it is necessary to put more value on a systematized application of units and their notation in text editors. Therefore, it is important to describe units of input quantities most completely. To arrive, for instance, in the example for measuring an activity, at the unit “Bq” as a part of the output quantity’s unit, the following is especially important:
Don’t leave the unit field of a detection efficiency empty, but use the unit string “1/Bq/s“;
Apply a unit like “Bq*s/kg” for a calibration factor;
For a chemical yield, if determined by weighing, the unit strings “g/g“ or “g/kg“ may apply.
Missing units of input quantities may prevent from calculating the output quantity unit correctly.
Important
Unfortunately, this automated way of calculating units is not compatible with applying trigger variables for scaling factors.
5.21.1. Collection of basic units and derived units¶
It is necessary to differentiate between basic units and derived units. For evaluating an UncertRadio project, the aim is to replace derived units by their basic units. Such a conversion requires to apply an associated conversion factor to values und uncertainties of the quantities.
The UncertRadio installation includes two txt files,
unitsTable.txt and units_other.txt. These are shown below.
unitsTable.txt (first part):
base:Base unit;base#: base unit value; syn:synonym;derv:derived
unit;conv: scale factor
base=Bq
base#=11.
derv=mBq
conv=1.00E-03
derv=µBq
conv=1.00E-06
derv=kBq
conv=1.00E+03
base=s
base#=21.
derv=min
conv=60.
derv=h
conv=3600.
derv=d
conv=86400.
base=1/s
base#=0.047619047619
derv=cps
conv=1.0
derv=cpm
conv=0.01666666666667
derv=cph
conv=0.000277777777778
derv=1/min
conv=0.01666666666667
derv=1/h
conv=0.000277777777778
base=kg
base#=41.
derv=g
conv=1.00E-03
derv=mg
conv=1.00E-06
...
units_other.txt (complete):
unit=Bq s
ubase=Bq*s
unit=m2
ubase=m^2
unit=m³
ubase=m^3
unit=cm2
ubase=cm^2
unit=cm3
ubase=cm^3
The scaling factor associated with a counting duration is used (by inversion) for a count rate variable R and, in most cases, this factor is the same for R and for u(R), as long as the Poisson statistics is applicable. An exception is given by the gross count rate discussed in chapter 6.10, which is the sum of a binomial and a Poisson distributed quantity. For a calibration factor w or phi, which can be treated as a generalized product, the scaling factors for w or phi and for u(w) or u(phi) are the same.
5.21.2. Explaining the calculation of units of dependent quantities¶
For a dependent quantity the procedure is based on its equation given to UncertRadio. The right-hand side of this equation is an arithmetic expression (formula) of variable names. For calculating a unit, in a first step, the variable names are replaced by unit names as strings; a variable name “eps“ for a detection probability, e.g., is replaced by “(1/eps/s)“; the brackets shall assure that this expression, after insertion into the equation, is treated algebraically correct. In a later step, the unit parts contained in it, “Bq“ and “s“, are replaced by the characteristic numerical values “11“ and “21“ given in column B of the file unitsTable.csv.
Before basic units can used for calculations, the following modifications remain to be applied:
the right-hand side of an equation with the number \(i\) consists of some quantities numbered by \(k\); the unit of the quantity with number \(k\) can consist of one or more unit parts. The \(k\)-th quantity has an index or address \(nng(k)\) within the completed symbol table within UR.
outside of arguments of function, all minus characters are replaced by plus characters; this shall assure that in case of a simple net count rate the difference of the unit values shall not become zero.
For functions used inside a formula, like Log(), Exp() and Sqrt(), the variable names inside their arguments are replaced by unit names and later by their characteristic unit values. In this was, the argument of such a function gets a form which can be calculated numerically. For this purpose, a second, simpler function parser is used UncertRadio, called seval, which can calculate the formula string, if containing only numbers, directly, it does not operate on variables.
If the argument of Log() (mostly 2) does not contain a variable with non-empty unit, i.e., a number, the expression Log(Argument) is set equal to 1.
The unit of an input quantity with number \(k\) can contain more than one unit parts, such that the unit represents a small formula. For a detection probability \(eps\), the unit could be 1/mBq/min. The unit parts are converted to basic units and the associated conversion factors are combined in the same way to build the conversion of this input quantity: in the example, the scaling factor of the combined unit is: \(uconv\left( nng(k \right)) = 1/0,001/60\ = \ 16,66667\), if the desired unit shall be 1/Bq/s.
To enable calculation, a unit string is build, for the example \(eps\), from the characteristic unit values (see unitsTable.csv): “(1/11.0/21.0)“.
Within an equation \(i\) (for a dependent quantity) every single variable name contained in it (number \(k\)) is replaced by such a string. The scaling factor \(uconv(i)\) for the quantity associated with equation \(i\) is determined from:
Herein, the string \(strgv1\) is the formula string of equation \(i\), in which the names of the symbols \(k\) are replaced by the product \(uconv\left( nng(k) \right) \cdot Messwert(nng(k)\) converted to a string; \(strgv3\) is the formula string of equation \(i\), in which the names of the symbols \(k\) are replace by \(Messwert(nng(k))\) converted to a string.
Note: Messwert() denotes the array of measurement values (called MVals() in this test).
Example for the Expression ( (LAMSR times TS times 60^0) / (1. - EXP(-LAMSR times TS times 60^0)) )
strgv1:
strgv3:
Unit Conversion:
It is assumed that the argument of an Exp function contains only quantities like a decay constant lambda (1/s) and a counting duration t (s). It is then allowed for this argument, that besides the characteristic unit values also scaling factors of \(60^{\pm 1}\), \(60^{\pm 2}\) or \(86400^{\pm 1}\) and at the same time also associated factors like \(60^{0}\), build from Trigger variables, may occur. If then the overall argument value is not an integer value and is not equal to \(60^{\pm 1}\), \(60^{\pm 2}\) or \(86400^{\pm 1}\), a unit error is assumed; otherwise, the whole Exp(Argument) expression is set equal to 1.0 (Exp(Argument)=1).
Often, the Exp() expression occurs in the form of Form (1.0 – Exp()). The Minus sign in it is replaced by a Plus sign. If the analysis of the Exp() expression alone led to the result that it was set equal to 1, the whole (1.0 – Exp()) expression is set equal to 1. This still requires finding in the string the position of the left (opening) bracket.
In the case of a sum in the argument of Sqrt(), e.g., for the variance of a net count rate with three terms with the unit (1/s^2), the value 3.0 * (1/s^2) is expected for the argument. If, in this example, the factor 3.0 is not obtained, but a non-integer value, it can be assumed that at least one of the three terms carries a differing unit. If, however, an integer-valued factor is obtained, the whole sqrt expression can be replaced by the unit 1.
Following the replacement of an algebraic function expression for equation \(i\) by substrings containing the characteristic unit values, a formula string should have been obtained (as a string RSeiteG2(i)), which can be evaluated by seval. The resulting numerical value is Evalue:
Arrived at this stage, it may have happened that some unities cancelled out.
The question then arises, how many – and which ones – basic units remain
to contribute to Evalue (Eq. (5.21.2))? Therefore, in this formula string, the individual unit values, like “21.0“ for “s“ string, are replaced by their basic units ( as strings). Based on pairs “Basic unit name, unit value“, which are taken from the first two columns of the file unitsTable.csv, the more complex function parser parsef can be used for calculating partial derivatives of the formula \(i\) with respect to the basic units. Only such individual units contribute to the unit of \(i\) which show partial derivatives having (practically) non-zero values.
Now, when the set of participating unit parts is known, e.g., “Bq“, “s“ and “kg“, it has to be found out, which of them belong to the nominator or to the denominator of a generalized product. For these three unit parts, abbreviated now by a, b and c, the following \(2^{3} = 8\) possibilities have to tested:
The 8 possible combinations are tested numerically; if one of it results in the above-mentioned value Evalue Eq. (5.21.2) ), the correct combination is found: e.g., “Bq*s/kg“, if the value Evalue is equal to 11.0*21.0/41.0.
5.21.3. Adjustments in the procedure¶
First, the units of all (independent) input quantities are replaced by basic units. If this implies a scaling factor not being one, the associate quantity value is (temporarily) multiplied with this factor.
In the next step, the units of the dependent quantities are calculated from the just treated input quantity units as described above.
The scaling factors of the dependent quantities are not derived from unit calculations. Instead, after the modification of the input quantities, they are calculated internally using the function Resulta without considering their units. Their associated unit scaling factors unit_conv_factor() are calculated thereafter, simply as ratios of the new quantity values and their previous values. Values of the uncertainties are then scaled by these factors unit_conv_factor().
5.21.4. Invoking the test of unit calculations¶
The calculation of units of dependent quantities cab be invoked under the menu item “Edit – test physical units“. The project should be developed such far that values are available under the TAB “Results”.
Important:
The calculation of units implies the conversion to basic units. If other basic units are desired, the latter must be declared as basic units in the file unitsTable.csv. For example, if the unit kg shall be replaced by the unit g, make g to the basic unit and the kg to a derived unit.
If the project contains a Trigger variable, invoking the unit test modus is prevented from invoking. The reason is, that a modified project saved directly by this test mode as a new file, normally does not work properly.
If the test modus still indicates errors, this modus must be finished with explicitly using the close button of the Editor Tab. This leads to restoring the original status of program data.
If no unit-related errors are shown, an addition button appears. It allows to save the modified state of the project as a new project file. This normally is necessary only if there are obvious deviations between the output quantity values.
The program executes the calculations according to Section 5.21.2 and then displays in the program editor a comparison for the list of symbols.
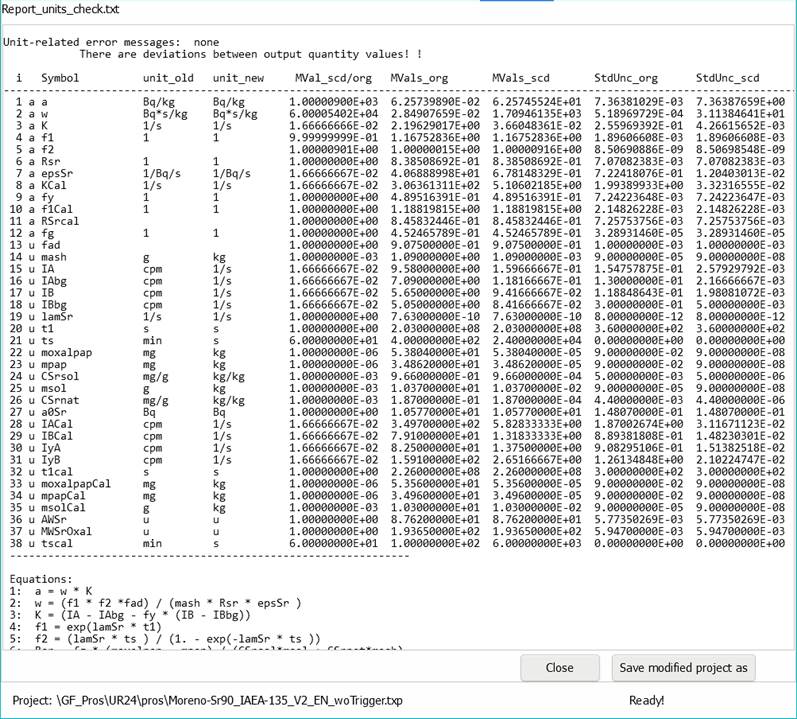
For dependent quantities (indexes \(i\)), the unit names given primarily by the user are replaced by “calculated“ unit names, which means that one must take care about the changed status of the project.
For the output of this test, UncertRadio calculates scaled values of measurement and associated standard uncertainties (MVals_scd und StdUnc_scd) as follows:
The column „MVal_scd/MVals_org“ shows the obtained actual scaling factors unit_conv_factor().
The values Mvals_scd (dependent), derived with the function Resulta from the modified (independent) input quantity values.
All values StdUnc_scd, by scaling the previous values StdUnc_org with the factors unit_conv_factor().
The output of the comparison test in the editor starts with a first error message, if the comparison between the value Evalue (Eq. (5.21.2)) and values from Eq. (5.21.3) (previous section) does not come to any agreement.
5.21.5. Introduction of Trigger variables¶
The program cannot give direct recommendations how to proceed if the test runs into an error. One reason can be a scaling factor which already exists in an equation like 60 for transforming “min“ into “s“. The impact by such already existing scaling factors can be reduced by using special switching variables (see section Section 1.2.6): for “Minutes (min)“ or for “Gram (g)“ already existing scaling factors 60 or 1/1000 are to be replaced as follows (alternatively, these factors are replaced by 1 and their unit is changed explicitly to “s” of “kg”):
60 60^min_Trigger
1/1000 1/1000^kilo_Trigger
These two special Trigger names are directly interpreted by UncertRadio; the value zero is assigned to them, if the Menu item „test physical units“ is applied, and prior to the test, they get the value 1.
The problem, that the expected unit of the output quantity, “Bq“ in the case of an activity, does not contain the substring “Bq“, but “1/s“ instead, can very often be solved by attributing the unit “1/Bq/s” to the detection probability.
Test example: Janszen-Sr-89-Sr-90_V2_DE.txp
The execution of the test stops with an error message. Then, the following changes are applied:
The first two equations:
a89 = As89 / (ms/1000.)
a90 = AsS90 / (ms/1000.)
are changed to:
a89 = As89 / (ms/1000.^kilo_Trigger)
a90 = AS90 / (ms/1000.^kilo_Trigger)
To obtain the desired unit “Bq/kg“, set the units of the four detection probabilities epsXXX to “1/Bq/s”.
The project file including these changes is available as Janszen-Sr-89-Sr-90_V3_DE.txp.
If a unit error is introduced, e.g., by changing in the symbol table under the TAB “Equations“ the unit of t2m0 from “s“ to “min“, then move the calculations forward to the TAB “Results”. An expected error message is then obtained when the unit test is called, in this case:
Error messages:
Eq. #=8 Error CLCU: Units in EXP argument do not match: seval=-60.0000000 arg(EXP)=-(1.0/21.0) * ( 6.000000E+01*(21.0))
Eq. #=4 RD89 = RSr - w*RY*f7 - Abl*(etaSr * epsSrSr89 * f1): no unit found! Einvor=1 RSide=RSR-W*RY*F7-ABL*(ETASR*EPSSRSR89*F1)
Similar changes had to be applied to the project Moreno-Sr90_IAEA-135_EN.txp.
The unit-strings “u (uamu)“ were replaced by “u“. Within the equations for the quantities a, w, f2 and epsSr, the two switching variables “kilo_Trigger” or “min_Trigger” were introduced. A unit “mg Sr“ was replaced by “mg“.
The project file including these changes is available as Moreno-Sr90_IAEA-135_V2_EN.txp.
5.21.6. Experiences with the option for calculating units¶
The experience with the option for testing or calculating physical quantities could be improved with the version 2.4.21. As such, this option could be integrated for the first time in the test with „QC-Batch-Test“, i.e., into the automatic evaluation run over all example projects. This allowed to identify some projects exhibiting specially selected units, for example,
Wuebbeler_Ex2*.txp (Ohm, Volt, Ampere)
Sterlinski*.txp (n-activation, unit ng/g).
For the projects Kessel*.txp and Calibration-of-weight-Cox*.txp (calibration of masses), deviating factors of 1000 were observed. The project Calibration-of-weight-Cox*.txp is still too complicated with respect to deriving units. For the projects Neutron-dose-Cox-2006*.txp, changes of the resulting value by a factor of 100 per 36 are observed from changes in the input quantity units.
These projects are left as they are.
A real unit error was observed with the four projects sumEval*V2*.txp (DE+EN). For their version V2, at that time, the output quantity unit was set Bq/m²t, however, the associated area of 400 cm² had not been changed to 0,04 m². This error of the V2 version now soon became obvious by the new test modus. The new project version shown with the correct units, but output quantity values changed by the factor 100x100, has been saved, while still being in the test mode, as version V3 projects.
From the project Moreno-Sr90_IAEA-135_V2*.txp, the triggers and the associated scaling factors of 60 or 1000 have been removed from the evaluation equations and the projects were then successful tested for unit calculations. With the processed derived units, the missing of the constant factors has been equalized. Value and uncertainty of the output quantity finally is left unchanged. The new project produced within the test modus is now released as a V3 version.
The same applied to the project Janszen-Sr-89-Sr-90_V3*.txp. The kilo_trigger and the associated of the mass (g) were removed. The missing factor of 1000 in the equations has been equalized by the unit calculations, value and uncertainty of the output quantity are left unchanged. A new version V4 of these projects have been produced.
