4.7. Low-Level Applications, (N+x)-rule¶
Important
In 2024 it turned out, that the (N+x)-rule is not clearly state in ISO 11929. Thus, the described implementation in UR might not be correct. Therefore, it is up to the user to decide to use it.
Very low numbers of counts N are Poisson-distributed instead of Gaussian-distributed. Using Bayesian methods it can be shown that counting rates derived from them then are Gamma-distributed. Taking a prior assumed as uniform (Weise et al., 2009) results in an expected value of the counting rate \(R\ \)which is characterized by \(\widehat{R} = (N + x)/t_{m}\ \)with a value of \(u^{2}\left( \widehat{R} \right) = (N + x)/(t_{m}^{2}\ ) = \widehat{R}/t_{m}\ \)for its variance. From this the recommendation follows, for the case of very low counting numbers, to replace \(N\) by\(\ N + x\), being designated as the \(\left( \mathbf{N + x} \right)\) Rule here which is long known from the literature.
The symbol x in (N+x) may be considered as a variable designated as GamDistAdd in UR. This results in a Gamma distribution of the variable (count number) associated with this rule, which from a Bayesian view results from a prior which is proportional to 1/ρ (GamDistAdd=0.0), to ρ-1/2 (GamDistAdd=0.5) or which is constant (GamDistAdd=1).
c=GamDistAdd |
(1-c) |
mean |
|---|---|---|
0 |
1 |
N+0 |
1/2 |
1/2 |
N+1/2 |
1 |
0 |
N+1 |
It is assumed here that this rule only refers to the gross counting rate Rg and to the background counting rate R0, because other types of counting rates usually are determined by other methods being less direct than a measurement. Within the UncertRadio dialog, the values of these two counting rates do not require modification, if the \((N + x)\) Rule is applied directly to the gross and background counting numbers, Nb and N0, respectively. Within the program code the following replacement rule is applied:
Directly before a program part which is doing calculations with the counting numbers:
Nb is replaced by the term (Nb+ GamDistAdd),
N0 is replaced by the term (N0+ GamDistAdd).
After that program part: these replacements are removed.
The default value of GamDistAdd is 1.
The application of the (N+x) rule to the two mentioned counting numbers is made available within the TAB “Values, Uncertainties” by selecting “(N+x) rule” as type of distribution.
Note: Only for counting number variables the (N+x) rule may be selected; it must not be selected for the associated counting rate variables. The latter are treated in this way internally and thereby are also gamma-distributed. This means, that this rule is correctly applicable only if a counting rate R is defined by an equation R=N/t containing the associated number of counts N. For N only a value is given by the user, while the field for the uncertainty must be left empty; this uncertainty obtained by the gamma-distribution is then calculated internally.
Two example projects (Gamma-Dist_EN.txp and Lira_gammdist_EN.txp) demonstrate the application of the (N+x) rule for the case of very low counting numbers.
Important
In anticipation of the new version of ISO 11929:2019 the application of the (N+x) rule has been modified as follows. Apart from a single exception, x=0 is used in (N+x). The exception is N=0: then x=1 is used. This requires that the variable GamDistAdd must be set to zero ( Options – Presettings). Under this prerequisite, x=GamDistAdd=0, UncertRadio internally adds 1 to N only if N=0 (this means “0+1”). This means that for N>0 a Gamma distribution is applied for the associated count rate R with a prior(R) ~ 1/R. In contrast, for N=0 a uniform prior(R) is assumed.**
If, however, x=GamDistAdd has been set a value > 0, which may be true for already existing UR projects, it will always be added to N, also for N>0.
It is assumed that the (N+x) rule may be used only with measurement procedures not requiring a linear least-squares method – and only in the case of very low counting numbers. For procedures using the least squares method applied to low counts the fitting result would be questionable; in that case where the Poisson distribution has to be used, the least squares method would be biased and e.g. the Poisson-Maximum-Likelihood-Estimation would have to be applied.
With the following example, based on Gamma-Dist_EN.txp, it shall be demonstrated that applying the MC simulation may result in asymmetric distributions deviating substantially from the normal distribution.
The equations may be as follows:
A = phi * Rn
Rn = Rg - R0
Rg = ng / t
R0 = n0 / t0
The (N+1) rule is selected for the quantities ng and n0.
The starting case may be given by: Phi = 1, urel(Phi) = 0,1, t =100 s and t0 = 500 s as well as ng = 8 counts and n0 = 6 counts, i.e. Rg = (8+1)/100=0,09 s-1 and R0 = (6+1)/500=0,014 s-1. The MC-Simulation leads to the following triple graph, showing a slight asymmetry of the simulated (green) distributions:
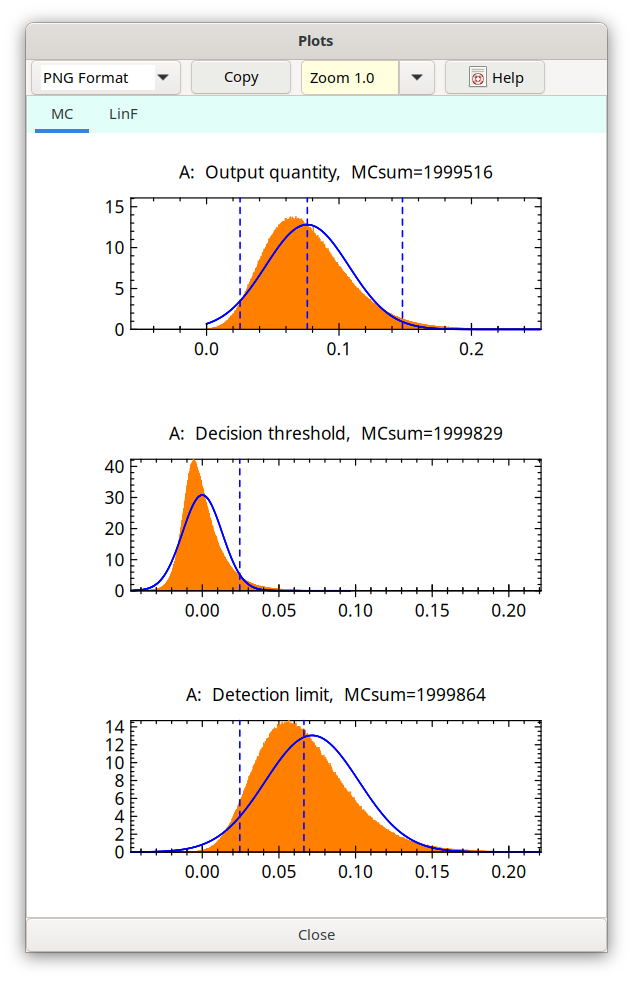
Fig. 4.7.1 Starting case¶
For the next case, with t0 = 500 s, but n0 = 0 counts, especially the distribution of the decision threshold (following triple graph) shows an even more pronounced asymmetry. This asymmetry is the reason that the MC value of the decision threshold is about the double of that of the analytical procedure (blue curve).
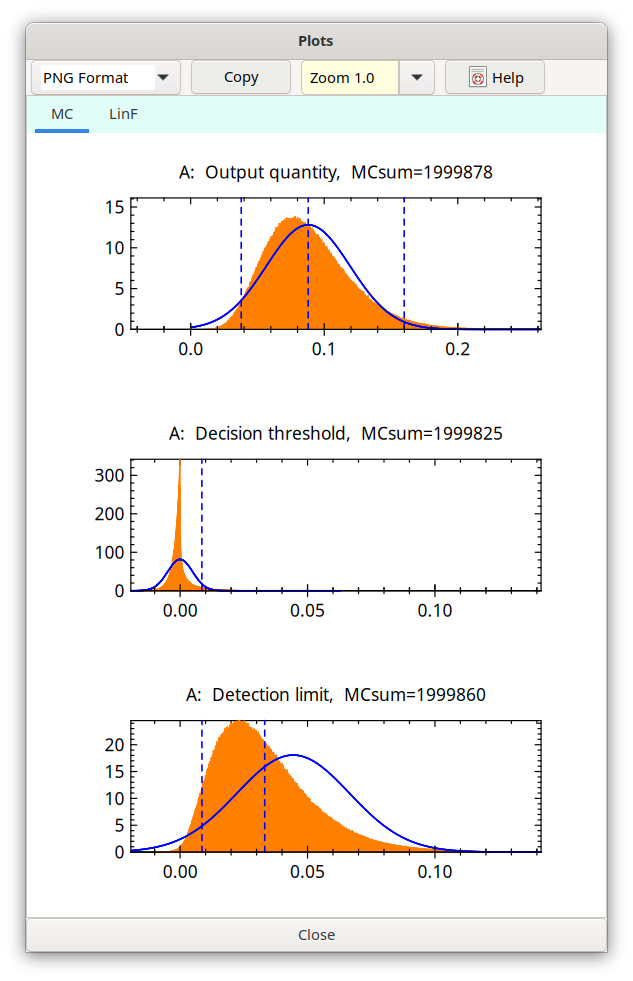
Fig. 4.7.2 n0 set to null¶
As a third case, compared to the starting case, only the background counting duration t0 is increased to a value of t0 = 60t = 10000 s (a case seldom encountered in practice), which makes the background counting rate R0 very small, especially for the decision threshold a very asymmetric distribution is obtained from which only a very small part is within the negative region. This shape arising from the Gamma distribution is quite different from what one is usually dealing with, e.g., shown under Obtaining MC distributions and statistics derived of it in detail.
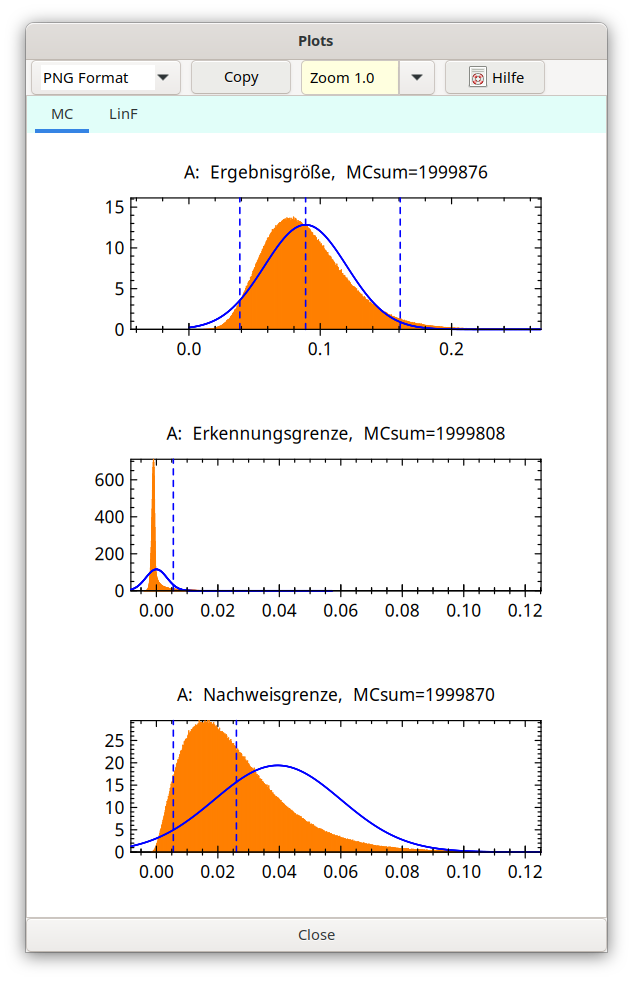
Fig. 4.7.3 t0 enlarged to t0=60 t¶
The reason is given by the fact that with such a small background counting rate the distribution of the decision threshold is mainly affected by the gross counting rate for which the Gamma distribution for very low counting numbers is very asymmetric and always has positive possible values.
